201
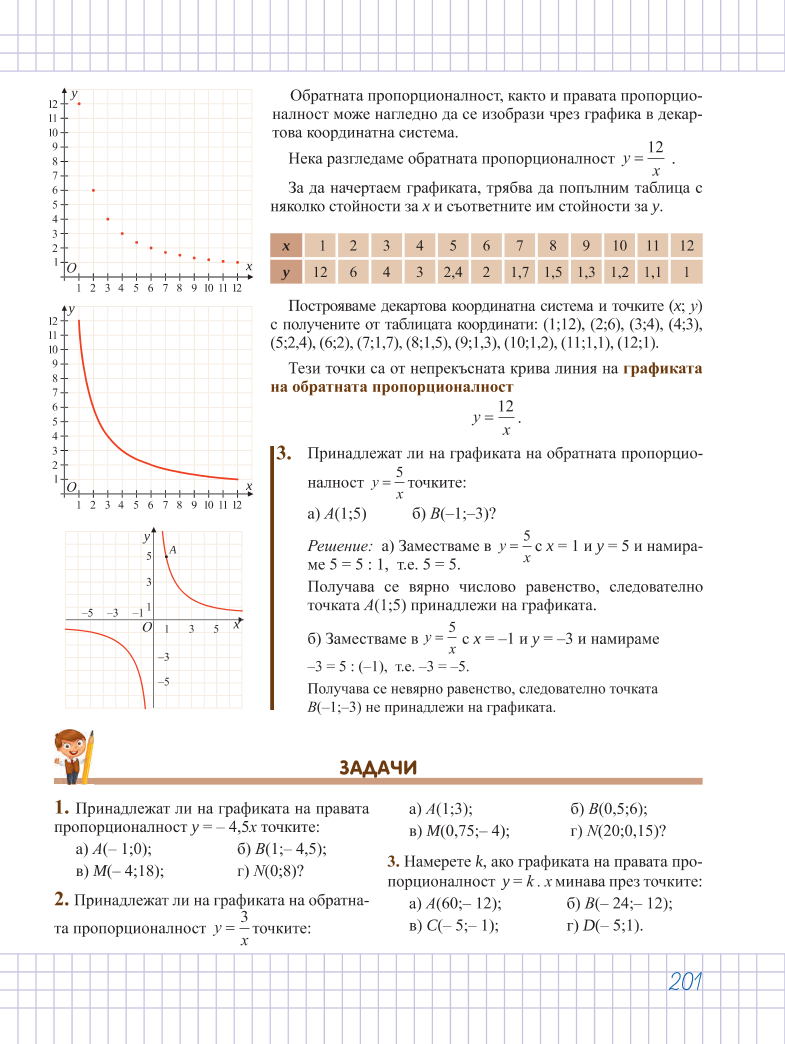
Нека разгледаме обратната пропорционалност
y
x
=
12
.
За да начертаем графиката, трябва да попълним таблица с
няколко стойности за
x
и съответните им стойности за
y
.
Построяваме декартова координатна система и точките (
x
;
y
)
с получените от таблицата координати: (1;12), (2;6), (3;4), (4;3),
(5;2,4), (6;2), (7;1,7), (8;1,5), (9;1,3), (10;1,2), (11;1,1), (12;1).
Тези точки са от непрекъсната крива линия на
графиката
на обратната пропорционалност
y
x
=
12
.
x
1
2
3
4
5
6
7
8
9
10
11
12
y
12
6
4
3
2,4
2
1,7
1,5
1,3
1,2
1,1
1
Принадлежат ли на графиката на обратната пропорцио-
налност
y
x
=
5
точките:
а)
А
(1;5)
б)
В
(–1;–3)?
Решение:
а)
Заместваме в
y
x
=
5
с
x
= 1 и
y
= 5 и намира-
ме 5 = 5 : 1,
т.е. 5 = 5.
Получава се вярно числово равенство, следователно
точката
А
(1;5) принадлежи на графиката.
б)
Заместваме в
y
x
=
5
с
x
= –1 и
y
= –3 и намираме
–3 = 5 : (–1),
т.е. –3 = –5.
Получава се невярно равенство, следователно точката
В
(–1;–3) не принадлежи на графиката.
3.
ЗАДАЧИ
1.
Принадлежат ли на графиката на правата
пропорционалност
y
= – 4,5
x
точките:
а)
А
(– 1;0);
б)
В
(1;– 4,5);
в)
M
(– 4;18);
г)
N
(0;8)?
2.
Принадлежат ли на графиката на обратна-
та пропорционалност
y
x
=
3
точките:
Обратната пропорционалност, както и правата пропорцио-
налност може нагледно да се изобрази чрез графика в декар-
това координатна система.
а)
А
(1;3);
б)
В
(0,5;6);
в)
M
(0,75;– 4);
г)
N
(20;0,15)?
3.
Намерете
k
, ако графиката на правата про-
порционалност
y
=
k . x
минава през точките:
а)
А
(60;– 12);
б)
В
(– 24;– 12);
в)
C
(– 5;– 1);
г)
D
(– 5;1).
1
2
4
6
7
8
9 10 11 12
5
3
1
2
4
6
7
8
9
10
11
12
5
3
y
x
О
1
2
4
6
7
8
9 10 11 12
5
3
1
2
4
6
7
8
9
10
11
12
5
3
y
x
О
1
–1
–5
–5
–3
–3
1
3
5
5
3
О
x
y
A